|
Solver FAQ
(ANSWER, PORFLOW, TIDAL and RADM)
A:The
flux of variable at a boundary is composed of a diffusive and a
convective component. The total flux of the variable,
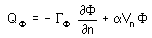
Where:
QF is the flux of F per unit area at the boundary.
GF is the
diffusion coefficient at the boundary,
n is the coordinate normal to the boundary,
a is a coefficient which depends on the
nature of the variable (for transport equations it represents the
density or the normalized density; for thermal transport, it
represents the density multiplied by specific heat of fluid),
and,
Vn is the velocity component normal to the
wall.
: GRAD means that
the gradient of the variable at the boundary is specified. The flux
of variable entering the boundary depends on two other quantities:
(1) the diffusion coefficient at the boundary and (2) velocity
across the boundary. Even if a GRAD = 0 command is specified, there
could still be a finite flux due to the velocity component.
: FLUX means that
the total value of flux (QF ) at the wall is specified. In this
case, by convention, a positive values means that the flux is
entering at the boundary and a negative value means that the flux is
leaving at the boundary.
Q: Should the flux printed under the “Total
inflow” (or “Total outflow”) category in the flux Balance Summary
match the sum of the Instantaneous Influx (or outflux) for the
individual boundaries.
A:Under
”total” categoriesare cumulative integrals with time. These will not
match the instantaneous fluxes. Only the time integral of the latter
should equal the “total” values provided factors such as
convection,diffusion, sources, decay and accumulation are all taken
account of.
For transient simulations, the values printed
For steady state simulations these two may be equal in many
situations. However there are a number of reasons these may not be
same. First the “total” values include effects of convection,
diffusion and sources. The flux printed under the “Total” category
is cumulative algebraic sum of all inflows (or outflows) for the
selected region. Whereas the flux printed at each boundary under the
“instantaneous” category is the algebraic sum of inflows for that
boundary. If a specific boundary has inflow at some nodes and
outflow at others, then only the net inflow will be printed.
Therefore the total inflow at the boundaries may not match the total
inflow for the subregion.
A: In
default mode of PORFLOW™, all mass
transport equation for each phase is converted to a corresponding
pressure equation in
“length” units. In SI units, the pressure will be in meters.
In multi-phase systems, the pressure for all phases is expressed in
terms of the pressure of the 1st (or primary) phase.
For example, for a 2-phase system, with water
as the 1st phase and oil as the 2nd phase, all pressure are in meters equivalent of
water. All boundary and initial conditions must be specified
in terms of meters of the primary fluid.
All sources (injection or withdrawal) are
expressed in volumetric units; that is in units of mass flow rate of the fluid
divided by its own density. For example in SI units, the mass
is in Kg, the density in Kg/m3 and the source in m3/s. Any
adjustment required to convert it to the volume of the primary fluid
is performed internally and is transparent to the user. PORFLOW™ further
allows the sources to be expressed in total rate (say m3/s), per
unit volume (say 1/s) or per unit area (say m/s), and in many other
forms. Please see the SOURCE command for different
options.
All mass input and output of fluxes at the
boundary is expressed in volumetric units; that is in units if mass
of the fluid divided by its own density per unit area of the
surface. For example in SI units, the mass will be in Kg, the
density in Kg/m3, the area in m2 and the flux will be in
m3/second/m2 (or m/second). The flux of each fluid is expressed in terms of
its own density and not the density of the primary fluid. Any
adjustment required to convert it to the primary fluid is performed
internally and is transparent to the user.
Q: What is the relation between
turbulence length scale used in ANSWER™ and the length scale used in
“standard” turbulence models?
A: A
definition of length scale used in in many turbulence models
is:
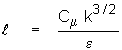
The definition used in ANSWER is:
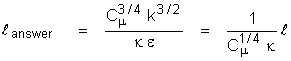
Here Cm is the viscosity constant (with a
value of 0.09 for the “standard” turbulence model) and
k is the von Karman constant (with a value
of 0.4187).
Thus with the “standard” set of k-e
constants, we get:
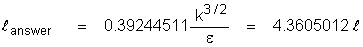
The reason for the use of the second
definition is that it leads to a simple relation for estimating
length scale close to a wall. From the log-law it can be shown that
in the vicinity of a wall in the fully turbulent boundary layer:
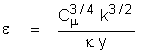
Where y is the distance from the wall.
Therefore the length scale as defined above is simply equal to the
distance from the wall in the vicinity of the wall.; that is:
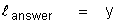
Q: What is the relation between
various turbulence quantities defined in k-e and k-w models?
A: The
basic definitions used in these models are as follows:
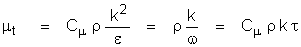
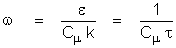
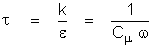
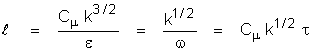
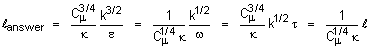
where:
k is
the kinetic energy of turbulence
e is
the dissipation rate of turbulence
w is
the turbulence vorticity fluctuation or frequency variable
t is
the turbulence integral length scale
l is
the “standard” length scale of turbulence
lanswer is the length scale of
turbulence used in ANSWER™ software
r is
the density of flow
k is
the von Karman constant
Cm is the constant in the eddy
viscosity relation With Cm = 0.09
and k =0.4187,
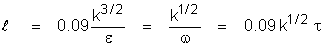
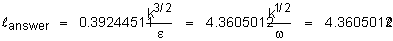
- Back To Top
Q: What is the
Convergence index and how is it computed?
A: The
convergence index is defined as:
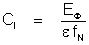
where:
CI is the convergence index,
EF is the computed error norm
(such as the matrix “residual” or flux “balance” disparity) for the
variable F,
e is
the convergence criterion controlled by the CONVergence command.
fN is the normalizing factor,
and
CI is a normalized measure of
convergence of the solution and has a value of unity when the error
norm in the solution is equal to the product of the normalizing
factor and the specified convergence criterion. By default EF is
set equal to mass flow disparity in the computational domain (see
FLUX command). This can be
changed to be the appropriate error norm for any of the variables by
the CONVergence command with
the REFErence modifier.
For PORFLOW™
and TIDAL™,
fN
is always set to unity. For ANSWER™ fN is set equal to the incoming
mass flow rate if the error norm is based on mass flow and the mass
inflow is non-zero; otherwise it is set equal to unity. It should be
noted that the default option in ANSWER is to select the error norm
as the mass flow disparity. This can be changed by a suitable
specification of the CONVergence
command with REFErence modifier.
- Back
To Top
For example:
CONVergence U ...
CONVergence
P …
A: Each convergence command specifies
the convergence criterion for a variable and the maximum number of
iterative steps that are performed to try and achieve convergence
for that variable. During the solution of each equation, the
convergence command for the dependent variable is invoked. Further
details for this command are given in the User’s Manual.
The overall iterative process for the
simulation is controlled by the chosen reference variable and its
convergence index. Default options for the reference variable are
given in the user’s Manual. The user can specify a reference
variable of choice by using the command mode:
CONVergence for variable P to be used as
REFErence ……
Q: What is the best type of residue to use on
the CONVergence command for a convergence criterion
?
A: There is no easy answer to this question. It
depends on the expected values of the variable and the nature of the
problem. The main choices are based on the local value of matrix
residual, normalized difference or absolute
difference:
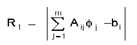
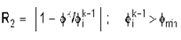
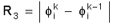
Either an average value of the sum at all
elements (GLOBal) or the maximum of the any local value (LOCAl) may
be specified:
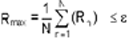
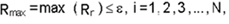
The R2 is a non-dimensional measure whereas the
other two are dimensional. R1 can suffer from the fact that changes
in F may be large even though R1 is small based on the values of
matrix coefficients. R2 exaggerates the changes for the smaller
values of the variables (for example a change from 1.E-15 to 1.E-16
will be shown as large even though both values are near machine zero
for 64 bit arithmetic. Similarly R3 exaggerates the upper end of the
values.
The global criterion may
indicate convergence while a region of the flow is still evolving
because it is averaged over all the elements. Also it may suppress
fluctuations when the number of elements becomes large.
The local criterion, on the
other hand, may exaggerate the effect of small changes in an
unimportant part of the flow whereas most of the flow has converged.
These points all should be kept in mind.
Please consult the User’s Manual for default choices. If one wants
to make sure that every value in the field has converged, then the
best index is the local normalized measure. For general use global
matrix residue is recommended.
-
Back
To Top
Q:
How do I judge if Convergence is achieved?
A: There are a number of factors that
affect the convergence of a numerical solution. There is no
universally acceptable criterion that has been developed to date to
uniquely define convergence. Often a combination of criteria must be
appealed to. To assist in this effort, ACRi software computes a
Convergence Index that is printed (by default) at each step of the
solution as part of the diagnostic output. This index is defined and
described in another section in this documentation.
In general one indication of convergence is
when the convergence index reaches a value of unity or less. This
means that the selected error norm has reached the specified
convergence threshold. However the convergence index alone is not
sufficient to ensure convergence. This is because the convergence threshold may
be too large or the error norm may not be sensitive enough to the
changes in the values of the variables. Therefore, it is also necessary to ensure
that that each of the selected diagnostic variables approaches or
converges to a unique value. These diagnostic values are printed by default
at each step of the diagnostic output. The user is provided a
control over the diagnostic values to be printed with the DIAGnostic
command.
In general the selected diagnostic values and
the location of the diagnostic node should be such that they
indicate the most sensitive location for ensuring convergence. For
example, for flows with embedded obstacles, often the nodes
immediately downstream of the obstacle are most sensitive to changes
in flow.
Certain selections are made in ACRI software
for default value of the error norm and the variable to be monitored
for convergence and its convergence threshold. Also by default
certain minimum and maximum iterations are performed for convergence
tests. Further, these defaults are problem dependent. These
selections may not be optimal for a given problem. Therefore the
user is cautioned to examine these defaults carefully and to use the CONVergence and DIAGnostic commands in a suitable manner to ensure
proper convergence of the numerical solution.
-
Back
To Top
Q: What values
should be used for RELAxation factors?
A: There
are no hard and fast rules.
For ANSWER™ software,
for u, v and w velocity components the values should never be higher
than 0.5. In general a value of 0.3 is recommended. For “properties”
such as density, viscosity (if these vary) a value of 0.7 is
recommended. For k & e (which may be dominated by large source
terms) a value of 0.5 is recommended. Finally, for temperature or
enthalpy and other scalars values between 0.7 and 1.0 are
recommended.
In PORFLOW™, the only
relaxation factor which is generally recommended is that for
saturation if steady state simulations are performed.
In general, the bigger the
grid the smaller the relaxation factors. The bigger the “source”
terms or ”non-lineariry” in the equations, the smaller the
relaxation factors.
Non-orthogonal grids generate “source terms”
from off-diagonal (skew) diffusion contribution. In general, the
higher the skewness, the higher the source terms. Generally the
hybrid and mixed grids (such as tetrahedral) generate more elements
and a higher skewness. In general you need anywhere from 2 to 6
times as many tets as hexes to get comparable accuracy. A ratio of 4
is adequate for most estimates. So when possible, it is better to go
with hex or brick elements.
-
Back
To Top
Q: What is the
difference between using BOUNDARY and SOURCE commands for input of
flux at the boundary: say between the two
commands:
BOUNDARY for T at Y+ of ID= TOP FLUX=
1.
SOURCE =1 per unit AREA for T at Y+ of
ID=TOP
A: Provided the Y+ boundary refers to the external
boundary of
the computational domain, these two are essentially equivalent. The
first command will add heat flux to the total flux coming in at the
boundary while the second command will add heat to the source
term.
It is
assumed here that the subdomain ID=TOP is defined such that it
includes elements just inside the top boundary. If the SOURce
command is used, then additionally the boundary flux at the external
boundary which abuts the must be set to zero (BOUNDARY for T at Y+ of ID=TOP
FLUX=0.)
The values printed
at the top boundary will differ
since the first option forces the wall temperature to be higher to
allow heat input.
For internal
boundaries of the computational domain the SOURce command should be used. The use of
BOUNDARY command is not
recommended.
Please see the example input data set T.051 for
further clarification on how to use these
commands.
- Back To
Top
Q: When I give the command:
REFErence P=101000
Are the
pressure values reported by the software relative to this pressure
or are these now absolute?
A: Pressure values
are always reported in the relative mode.
Currently this command sets a reference pressure that is not
used. In future versions of ACRi Software (starting with 5.03)
this command will set the gas base pressure.
The gas pressure (say, for
computing density by gas law) can be set by the command:
GAS base pressure P =
2.E5
- Back To
Top
Q: When I give the command:
REFErence T=273.15
ABSOlute
Are the
temperature values reported by the software relative to this
absolute?
A:
Yes. Temperature values are always reported relative to this
value. The temperature (say, for computing density by gas law)
is computed as the reported temperature plus this absolute
value.
- Back
To Top
Q: How do
I compute flows with natural convection in
ANSWER?
A: There are three alternative
ways:
1. Boussinesq
Approach. This mode is invoked by the PROBLEM BOUSSINESQ
command. In this mode density is assumed constant except for a
"buoyancy" term in the momentum equation in the direction of the
gravitational acceleration. See
problem B.02 in ANSWER™ Examples
.
2.
Direct Source in Momentum
Equation. This mode is invoked by a SOURCE command in the
relevant momentum equation. See problem B.03 in ANSWER™
Examples .
3.
Coupled gravity and Variable
Density. This is the most comprehensive and mathematically
exact formulation. See problem B.04 in ANSWER™
Examples .
Example of each type is given in the B.02, B.03 and
B.04 data set, respectively. The 1st and 2nd modes are essentially
linearizations of the coupled mode. These should be tried to get a
feel for the problem. In fact often these are good approximations
provided the density change is less than a few percent. These are
generally more stable than the fully coupled mode. Natural
convection flows are notoriously "unstable" and often have multiple
"solutions". There is no guarantee of uniqueness of solution for
natural convection flows and in fact experiments suggest both
non-unique and chaotic solutions for even simple
geometries.
- Back
To Top
Q: How do
I obtain values of variables at a boundary or a
surface?
A: Please see
the:
WRITE command with boundary
mode
- Back
To Top
Q: How do I obtain values of fluxes at a
boundary or a surface?
A: Please see
the:
PRINT command with FLUX
mode
and the
WRITE command with boundary
mode
- Back
To Top
Q: How do I
vary Viscosity in ANSWER™ computations?
A:The reference value of viscosity in
ANSWER™ is set by
the VISCOSITY command. Any turbulence contribution is
automatically computed from the active turbulence model and added to
these values. The values so computed can be replaced by using
the DIFFusion coefficient or CONDuctivity command. Examples
are:
DIFFUSION coefficient for U is 0.0034
Or:
DIFFUSION coefficient for U is a LINEAR function:
0.0034 + 0.001 * T
Please see the VISCOSITY, DIFFUSION and
CONDUCTIVITY commands
for further elaboration and other available options. The
value, if it is varied, must be set for each of the velocity
components.
- Back
To Top
Q: How do I vary thermal conductivity in
ANSWER™ computations?
A: There are two ways to control thermal
conductivity in ANSWER™. To start with
the thermal conductivity is computed from the effective viscosity
and the Prandtl number of the fluid; that
is:
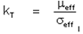
where the fluid viscosity and
Prandtl number can be set by the VISCOsity and PRANdtl number
commands.
The value
of thermal conductivity computed above is overwritten by the values
specified by the CONDuctivity command if any such command is
specified. Examples are:
CONDuctivity for H is
0.0034
Or:
CONDuctivity for H is a LINEAR function:
0.0034 + 0.001 * T
Please
see the VISCOSITY, PRANDTL and CONDUCTIVITY commands for further
elaboration and other available options. See problem T.052 in ANSWER™ Examples.
- Back
To Top
Q: Can I
overwrite the computed values with values by my own
algorithm?
A:Yes. The SET, FIX, READ and INITial
commands are available and
they can be used together or
separately.
The
SET
command can be used to set the
values of any variable in any subregion of the computational
domain. It provides a very versatile option to set the
variable to a constant, a function or arbitrary values.
Multivariate functions can easily be implemented by successive
use of multiple SET
commands.
By
default the SET command only sets the value of a variable at the time
of its implementation. If the variable (to which the
SET
command applies) is a function
of time or other dependent variables, then the
SET
command must be used with the
ALWAYS
modifier. With this
modifier, the value of the variable is freshly computed at the start
of each time (or iteration) step.
The variables for which a differential transport
equation is solved (or directly derived variables such as
Temperature and Length scale for ANSWER software) an additional step is
needed to “fix” the values of the variable.
A
corresponding FIX
command must be given for the
subregion for which the SET
ALWAYS
command is given.
The FIX command is interpreted as a command to
“skip” the computation of a variable from its governing transport
equation. Thus whatever value currently prevails is returned
as the value of the variable by the solution process. The FIX
command cannot be used for a
variable for which a transport equation is not solved
.
The READ
and INITial
commands can also be used to
set the values of a variable. These commands are more specific
in nature and less versatile than the SET
- Back
To Top
Q: How do
I obtain average values of a variable or its statistics for a sub
region of the computational domain?
A: Please see the:
PRINT command with STATISTICS
modifier,
PRINT command with AVERAGE
modifier,
STATISTICS command
and the
OUTPUT command with STATISTICS
modifier
- Back
To Top
Q: What elements
are contained in a LOCAte command specified with grid indices for a
structured grid?
A: There are three
distinct cases:
(a)
The indices include boundary nodes: The locate command selects all active nodes at
the boundary plus field nodes (elements) immediately next to the
boundary. For a 2D structured 22 by 12 grid if the specification is:
LOCATE (1, 1) to (1,
11) as
ID=LEFT
Then the selected nodes are the boundary nodes:
(1,2), (1,3),
(1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (1,10) and
(1,11)
Plus the
field nodes:
(2,2), (2,3),
(2,4), (2,5), (2,6), (2,7), (2,8), (2,9), (2,10) and
(2,11)
Plus the
two boundary nodes located at:
(2,1) and
(2,12).
The
corner nodes (1,1) and (1,12) are decorative nodes and do not appear
in the computations; these are omitted.
(b)
The indices refer to field nodes adjacent to boundary: In this case the locate command
selects all the field nodes plus boundary nodes immediately next to
the field nodes. For a 2D structured 22 by 12 grid, if the
specification is:
LOCATE (2, 2) to
(3, 11) as ID=LEFT
Then the
selected nodes are the field nodes:
(2,2), (2,3), (2,4), (2,5),
(2,6), (2,7), (2,8), (2,9), (2,10) and (2,11) (3,2), (3,3), (3,4),
(3,5), (3,6), (3,7), (3,8), (3,9), (3,10) and (3,11)
plus the
boundary nodes:
(1,2), (1,3),
(1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (1,10) and
(1,11)
Plus the
four boundary nodes located at:
(2,1) (3,1), (2,12) and
(3,12).
(c)
The indices refer to field nodes away from boundary: In this case the locate command
selects only the field nodes. For a 2D structured 22 by 12 grid, if
the specification is:
LOCATE (3, 3) to (4, 10)
as ID=BLOCK
Then the
selected nodes are the field nodes:
(3,3), (3,4),
(3,5), (3,6), (3,7), (3,8), (3,9), (3,10) (4,3), (4,4), (4,5),
(4,6), (4,7), (4,8), (4,9),
(4,10)
- Back To
Top
|